Second Normal Form (2NF)

2nd Normal Form Definition

A database is in second normal form if it satisfies the following conditions:

• It is in first normal form
• All non-key attributes are fully functional dependent on the primary key

In a table, if attribute B is functionally dependent on A, but is not functionally dependent on a proper subset of A, then B is considered fully functional dependent on A. Hence, in a 2NF table, all non-key attributes cannot be dependent on a subset of the primary key. Note that if the primary key is not a composite key, all non-key attributes are always fully functional dependent on the primary key. A table that is in 1st normal form and contains only a single key as the primary key is automatically in 2nd normal form.

2nd Normal Form Example

Consider the following example:

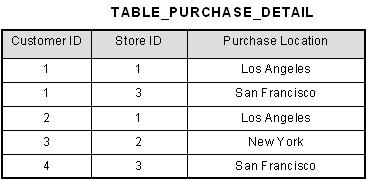
This table has a composite primary key [Customer ID, Store ID]. The non-key attribute is [Purchase Location]. In this case, [Purchase Location] only depends on [Store ID], which is only part of the primary key. Therefore, this table does not satisfy second normal form.

To bring this table to second normal form, we break the table into two tables, and now we have the following:

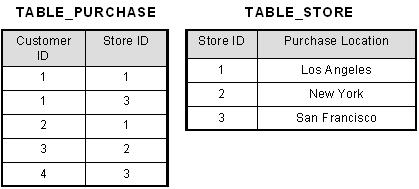
What we have done is to remove the partial functional dependency that we initially had. Now, in the table [TABLE_STORE], the column [Purchase Location] is fully dependent on the primary key of that table, which is [Store ID].

Return to Database Normalization
Other Normal Forms:   First Normal Form   Third Normal Form